Designing Medieval Vaults: the Mathematics of Rib Geometries

Though the Tracing the Past project has focused primarily on the practical study of medieval vault geometry, it has also been useful to consider its theoretical side. Whilst algebraic approaches to geometry were beginning to be studied during the twelfth and thirteenth centuries (facilitated by the extensive translation of Arabic texts), they do not appear to have been known by architectural designers. Nevertheless, an algebraic study of vault geometry can help us to understand the more practical side of how medieval vaulting was devised, especially when exploring what options were available to medieval masons for realising their designs.

Geometrical properties

Whilst the end result of a vault’s design was undeniably three-dimensional, the forms of its individual parts were set out entirely using two-dimensional geometry. Each rib was essentially designed through the medium of two intersecting planes, a horizontal plane representing the vault’s plan and a vertical plane representing its curvature. Within these planes, each rib has a discrete set of mathematical properties which allow its shape to be defined.

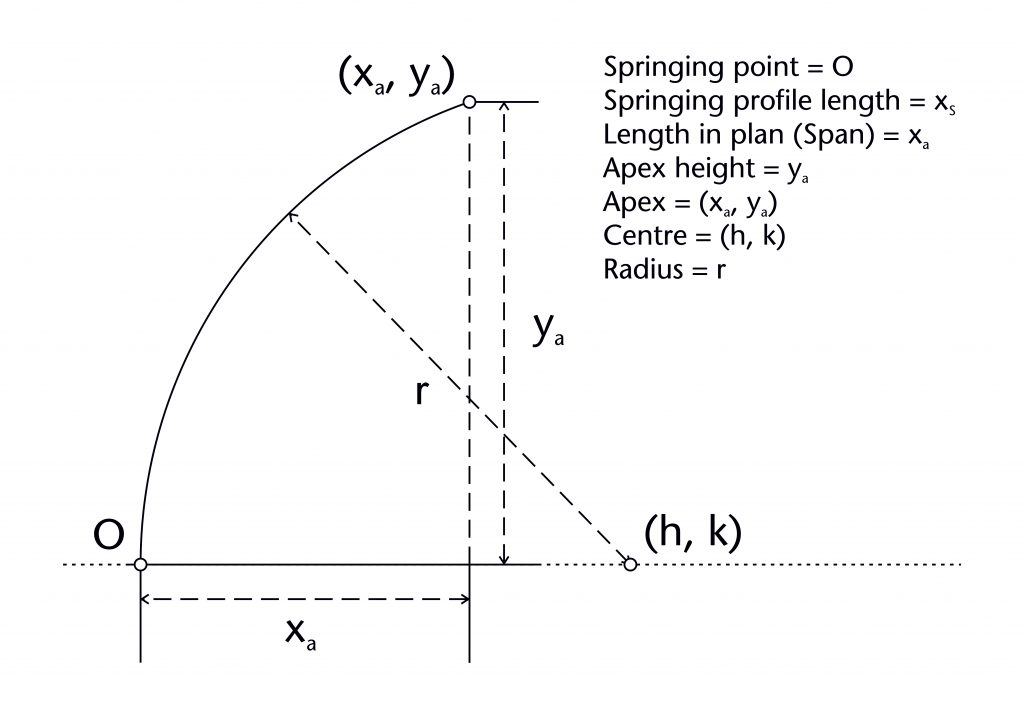
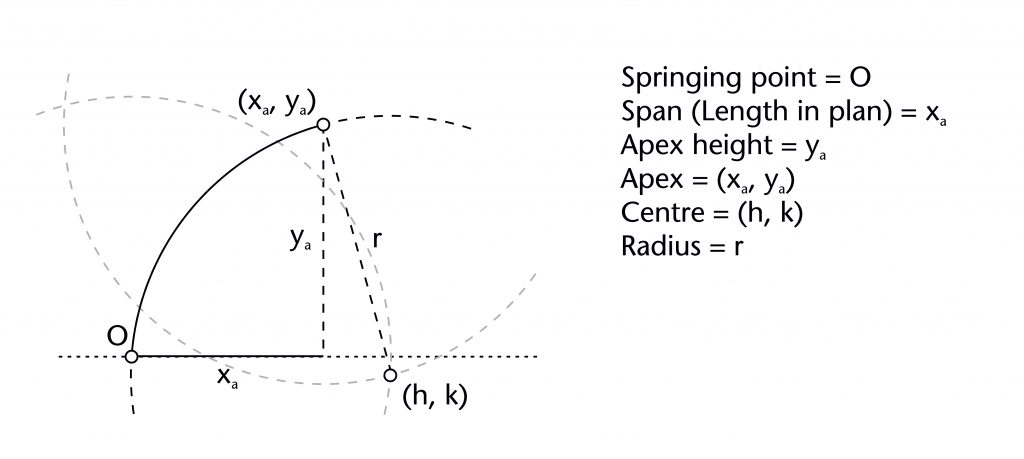
The first of these is its springing point (O). In most cases this is located at the level of the abacus of the supporting capital, though for liernes or ridge ribs it might be at a point of intersection with another rib. Sometimes the springing of the rib is stilted, meaning that it was slightly higher than abacus level. The vertical position of the springing point is referred to as the impost level (i).

The second is the apex or end point of the rib (x_a, y_a). Its position is located using two distinct variables, the apex height (y_a) defined within the rib’s vertical plane and the span (x_a) derived from the vault plan. In most cases the end point is covered by a sculpted boss, though there are some rare exceptions such as the south transept vault at Gloucester Cathedral. Sometimes the end point of the rib is equal to or lower in height than its springing point, especially within ridge ribs.

If the rib intrados consists of a straight line, then it will have a distance (d) from springing to apex. However, if the rib is curved then it will have both a radius (r) and a centre (h, k). The centre is defined using two components – a horizontal component representing its horizontal distance from the springing point (h) and a vertical component representing its vertical distance from the impost level (k).

All of these variables are mutually interdependent, as can be demonstrated by modelling the curvature of the rib using a two-dimensional co-ordinate system on its vertical plane. The origin (0, 0) is given by the springing point (O), with x representing the horizontal axis (span) and y the vertical axis (height). Within this system, the curvature of a rib can be modelled as a circle with a circumference passing through the springing point (0, 0) and apex (x_a, y_a) of the rib itself.

The general equation for a circle centred on the point (h, k) is as follows:

At the springing point (O), y = 0 and x = 0

At the apex point (x_a, y_a), x = x_a and y = y_a

Consequently, if both r² = h² + k² and r² = (x_a-h)² + (y_a-k)² are solved as simultaneous equations:

Whilst such an equation may appear complex, its practical implications are relatively straightforward. None of the variables listed above can be altered is isolation, as every modification will inevitably result in changes to at least one other variable within the system. Furthermore, it is clear that none of the relationships between variables are linear, meaning that even small changes could have potentially large effects on the geometry of the whole.

In order to design a rib within this system, it would therefore be necessary to convert these variables into fixed values. The simplest method for achieving this was to define variables using the features of the surrounding architecture. Spans (x_a) would invariably be defined by the vault plan, radii (r) could be transferred from other ribs or arches and apex heights (y_a) could be provided by nearby windows, crossing arches and other architectural features. However, this would necessitate four out of the five variables to be defined in advance for each an every rib, something which was not always possible for medieval designers. A far more practical solution was to use a geometrical method to set up additional relationships between the variables, allowing fewer fixed elements to be used to determine the values of the remaining variables.

Chord method

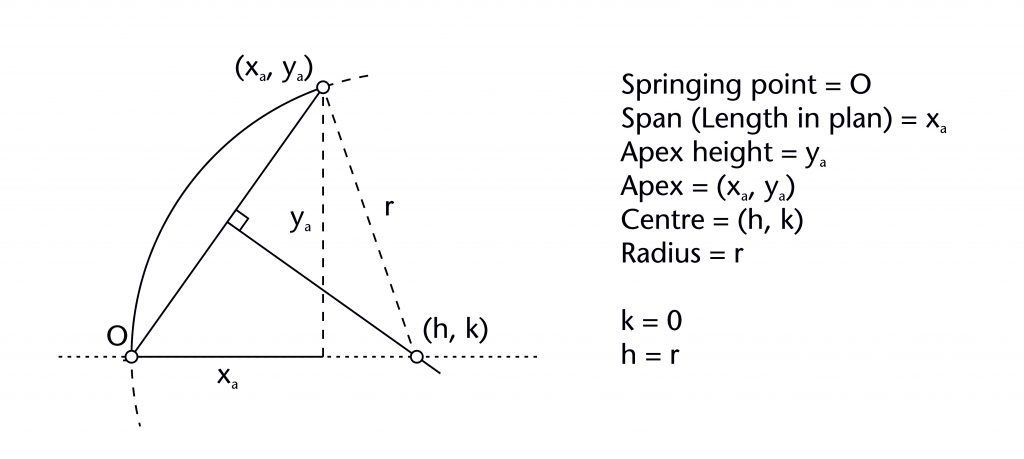
The chord method involves drawing a straight line between the defined springing (O) and apex points (x_a, y_a) of the rib. The horizontal position of the centre (h) is determined by identifying the point of intersection between the perpendicular bisector of this chord with the impost line, effectively fixing the height of the centre at the level of the impost (k = 0). Once the horizontal position of the centre is found, the radius (r) is also defined and the curvature of the rib can be drawn into place.

Considered mathematically, the method provides a means of using three fixed elements (span (x_a), apex height (y_a) and vertical position of centre (k)) to define the remaining two - the horizontal position of the centre (h) and the radius (r). Within our co-ordinate system, the chord extending from springing point (O) to apex (x_a, y_a) is given by the following linear equation:

At the springing point (O), y = 0 and x = 0

The gradient of the line (m) = y_a/x_a

Consequently, for the perpendicular bisector of the chord:

At the point of intersection between the perpendicular bisector and the chord, y = y_a/2, x = x_a/2

When the chord method is used, the centre for the circle (h, k), is therefore given by the point of intersection between the chord y = -(x_a/y_a)x + 1/2(y_a - x_a²/y_a) and the line y = k.

Consequently, if y = k, then x = h

As the value of k has been determined in advance, the equation can be rearranged to solve for h:

As the general form of the equation for a circle centred on (h, k) is r² = (x - h)² + (y - k)², and the arc of the rib passes through the springing point (y = 0, x = 0):

If the vertical position of the centre is fixed at the level of the impost (k = 0) then many of these terms can be dispensed with entirely, leaving the equation:

As the radius is not a fixed variable, the geometry of the entire rib is therefore determined solely by the relationship between the span (x_a) and apex height (y_a). Any increase to the rib's height or span would result in a corresponding increase in its radius, whereas any decrease would have the opposite effect. The relationship between these three variables, however, is not linear and consequently the effect on the radius is different depending on the magnitude of the change.

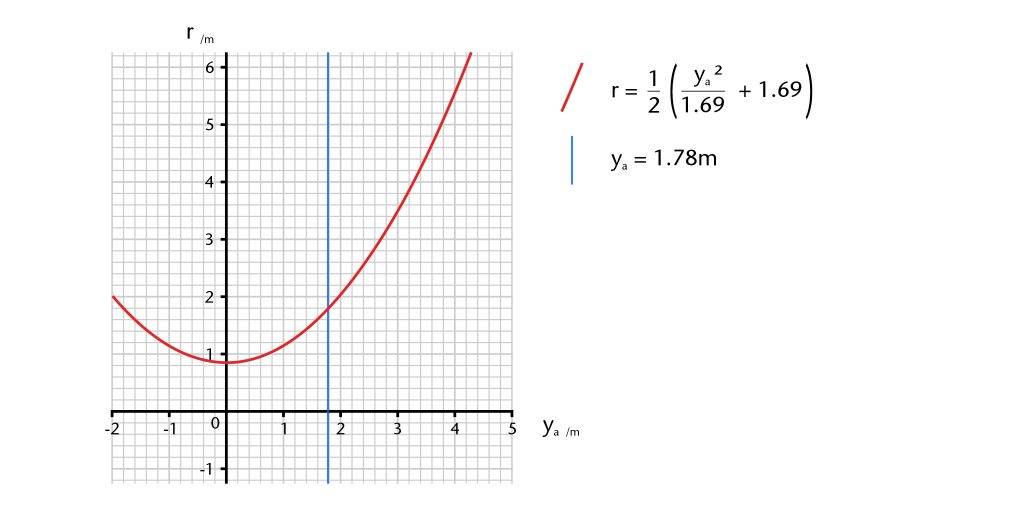
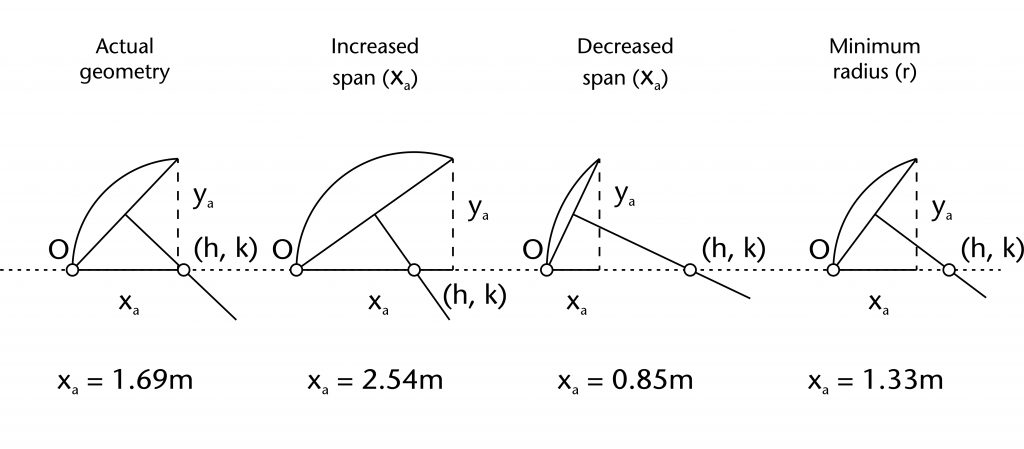
The most straightforward form of variation available to medieval masons was changing the apex height. This could be accomplished either by redefining the apex point of the vault or by changing the height of the springing point using stilting. Stilting the springing point by a set distance (x_s) would effectively lower the apex height by the same amount (x_a - x_s). The effects of such changes can be displayed graphically, in this case using the data for the wall ribs in the east walk of the cloister at Wells Cathedral.

The wall ribs in Wells Cathedral Cloister were probably constructed using the chord method. The apex height of the ribs (y_a) averages 1.78m, the same value as the average width of the bay. This suggests that the apex height of the bay was originally fixed using the vault's plan, specifically at half the width of the bay. However, due to the springing profile the span of the rib (x_a) is slightly smaller, averaging 1.69m. As the graph below shows, any increase or decrease to the apex height would result in an increase or decrease to the radius (r). However, the relationship between these two variables is not linear, but instead follows a parabolic curve with a minimum value for the radius equivalent to half that of the span (x_a/2) at y_a = 0. If the apex height (y_a) is lower than the radius, then the curvature of the rib would bulge upwards, eventually becoming semicircular at y_a = 0. Medieval designers seem largely to have avoided ribs that bulge in this manner, meaning that the apex height will normally be greater than the radius for chord method ribs.

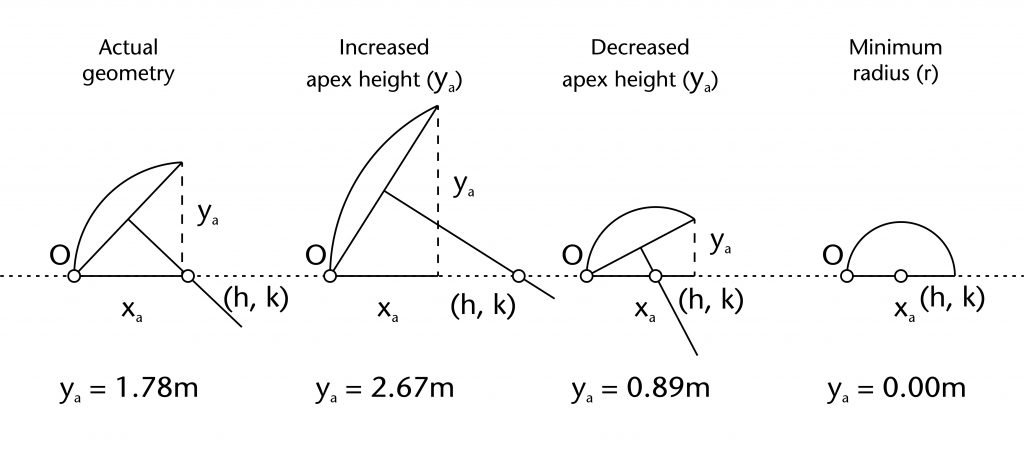
By contrast, if the span (x_a) or height of the centre (k) are varied, entirely different graphs are produced. The parabola for altering the span (x_a) shows that any decrease or increase in span would result in a corresponding increase in the final radius (r). If the span was reduced, the radius would increase at a faster rate than if it was expanded, as indicated by the difference in gradients between the left and right sides of the parabolic curve. Yet despite this, the graph shows that any small fluctuations in span from bay to bay would have a minimal effect on the final radius, meaning that the design would be relatively stable throughout the run of vaulting.

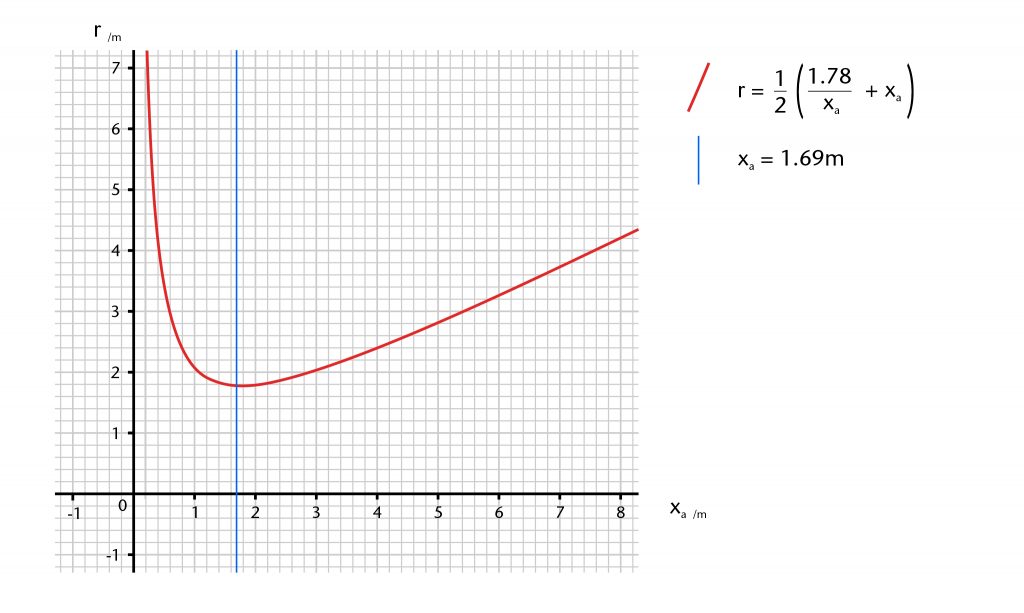
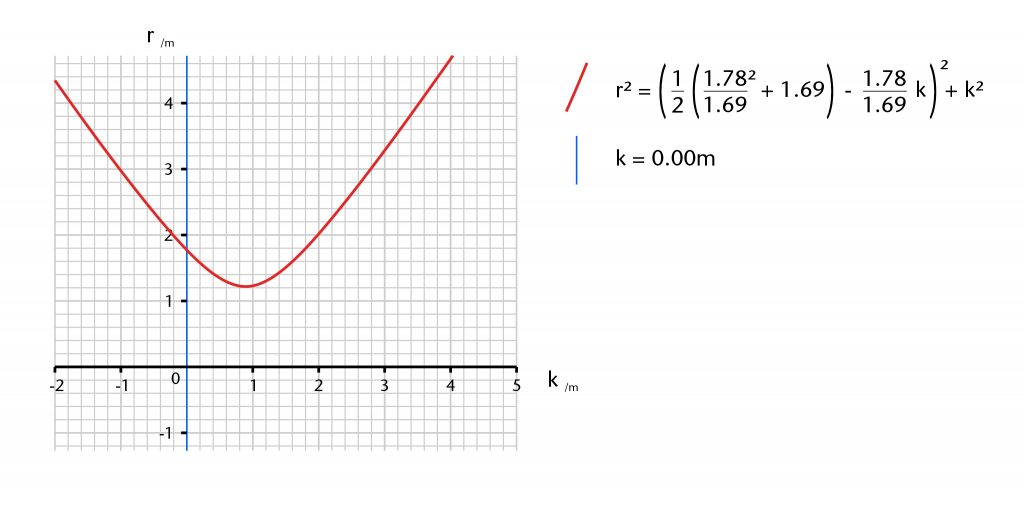
If the height of the centre (k) is varied, an entirely different graph emerges. When the height drops below the level of the impost (k < 0), then the radius (r) starts to increase. If, however, the height rises above the impost (k > 0), then the radius (r) will decrease down to a minimum of 1.23m at k = 0.89m. At this point the position of the centre would be located at the midpoint of the chord, with a height equivalent to half the fixed apex height (y_a). After this point (k > 0.89m), the radius will again start to increase, with no theoretical maximum. However, the rib would continue to bulge upwards, resulting in a visually awkward and structurally problematic ballooning effect.

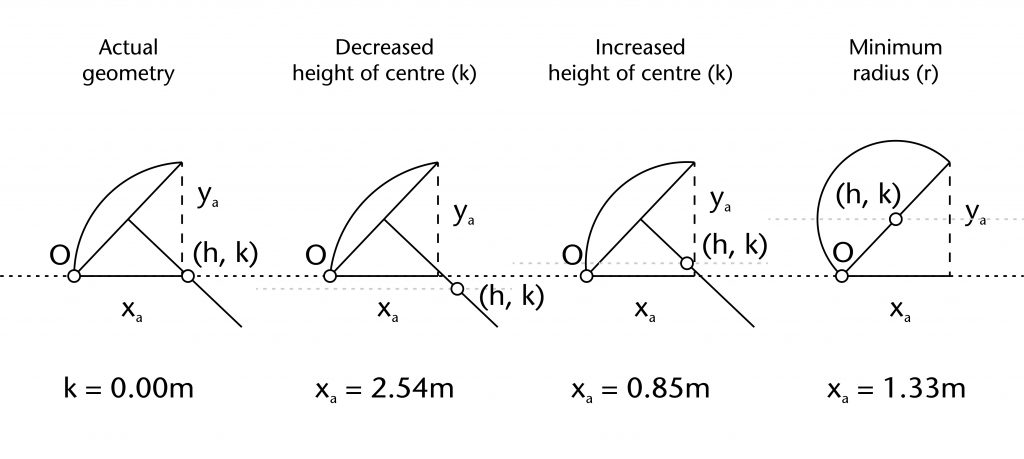
Few if any of the more extreme modifications to a rib's form that have been discussed above would be implemented in an actual vault design. However, this process of exaggeration does help to identify the kind of small scale fluctuations which occur regularly within our data. Minor accidental deviations in the span, impost level, apex height and height of the centre from bay to bay would have a minimal effect on the final radius for a rib constructed using the chord method. However, slightly larger deliberate changes could have a sizeable impact on the vault's final form. This was especially noticeable when altering the height of the centre, where the changing gradient of the parabola is noticeably steeper than that of the apex height or span.

Such an approach can be seen in the nave vault at Exeter Cathedral. In this case, the height of the centre (k) for the ribs constructed using the chord method was deliberately modified, alternating between one level above and another below the impost. As the level of the centre adjusted above and below the level of the impost, the profile of the ribs is alternately pushed forwards or backwards, resulting in an undulating fan of tiercerons spreading out across the vault's surface.

Three circles method

The three circles method involves drawing two circles of the same radius (r), the first centred on the springing point (O) and the second on the apex point (x_a, y_a) of the rib. The centre (h, k) is defined using the lower point of intersection between these two circles. This can then be used to draw a third circle of the same radius (r), providing the curvature for the rib.

For the three circles method, the position of the centre (h, k) is not therefore defined at the outset, but is instead determined by a geometrical process. Considered mathematically, it can be seen as the point of intersection between two circles given by the following two equations:

For a circle of radius r, centred on the springing point (0,0):

For a circle of radius r, centred on the apex point (x_a, y_a):

As the value of r is constant for both circles, these can be treated as simultaneous equations:

If the values of the span (x_a) and apex (y_a) are fixed, then the position of the centre (h, k) is solely determined by the magnitude of the radius (r). Furthermore, the values of h and k would be in linear proportion to one another, meaning that they would both be mutually interdependent. If the span or apex height were altered, however, the result would be a change in the position of the centre (h, k). Whilst this would not change the fixed radius (and therefore the curvature) of the rib, it would alter the positioning of that radius relative to the springing point (O), changing the three-dimensional form of the vault.

Such an observation has a number of practical implications for the process of vault design. In vaults where the same radius was used repeatedly for multiple ribs, the designer would need to take care to ensure that the resulting changes in apex height or span did not have a distorting effect on the curvatures of the ribs. It is perhaps for this reason that the two circles method was employed for the southwestern bays of the choir aisle vaults at Wells Cathedral, where the apex height (y_a) for many of the ribs was not defined at the outset. This meant that the only variable affecting the shape of the rib was its span (x_a), allowing the designer to modulate the final deign where necessary solely by altering the vault's plan.

Whilst medieval masons would not have possessed the mathematical knowledge necessary to understand these principles algebraically, this does not mean that they did not become aware of them through practical experience. Geometrical experimentation was fundamental to the developmental process of medieval architectural design, and the same principals which can be calculated mathematical could equally be demonstrated practically through the use of compasses, squares and straight edges. Consequently, though mathematics may not be an effective tool for revealing how medieval designers worked directly, they are nonetheless useful for revealing the kinds of problems and opportunities which were presented by the art of geometry.